AI摘要:This article discusses the use of acceptance-rejection sampling to simulate the near-wall gas normal velocity distribution in thermal equilibrium, providing a Python code example and resulting graph.
Powered by AISummary and Kimi.
Powered by AISummary and Kimi.
处于热平衡态的气体分子的速度满足一个非常优雅的分布—— Maxwell 分布,它在空间中三个方向上能分解为三个高斯分布(正态分布),如果需要对这样的分布进行抽样,在 python 中使用 random.gauss(μ,σ) 即可轻松达成。
而当大量气体分子在固体壁面附近处于平衡状态时,它同样具有一定的分布,仍然可以称之为 Maxwell 分布,也有一些文献称为 corrected Maxwell–Boltzmann distribution 或 half-range Maxwellian distribution。由于这时分布发生了变化,垂直于壁面方向(壁面的法向)不再满足高斯分布,因此这里使用接受拒绝采样(Acceptance-Rejection Sampling)方法进行抽样。
法向速度分布:
$$ f \left( v_{z} \right) = 2 \left( \frac{m_{gas}}{2 k_{B} T_{gas}} \right) v_{z} e^{- \frac{m_{gas} v_{z}^{2}}{2 k_{B} T_{gas}}} $$
python 实现10万次抽样:
# -*- coding: utf-8 -*-
import random
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
T_GAS = 300
kB = 1.380649e-23 #1.380649e-23J/K=1.987204e-3kcal/(mol`K)=8.617333262145e-5eV/K
MASS = 39.948
NA = 6.02214076e23 #u = 1.66053886e-27#1.66053886×10^-27 kg
u = 1.66053886e-27
sigma = (kB * T_GAS / (MASS*u)) ** 0.5
vz_maxwell = []
for i in range(0, 100000):
vz_sg = 0
vz_tmp = 10000
c = 2
while (vz_tmp > ((2*vz_sg*(MASS / 1000 / NA)/(2*kB*T_GAS))*np.exp(-(MASS / 1000 / NA)*vz_sg*vz_sg/(2*kB*T_GAS)))/(c*((MASS / 1000 / NA)/(2*np.pi*kB*T_GAS))**0.5*np.exp(-(MASS / 1000 / NA)*(vz_sg-250)*(vz_sg-250)/(2*kB*T_GAS)))):
vz_sg = random.gauss(250, sigma)
vz_tmp = random.uniform(0,1)
vz = vz_sg
vz_maxwell.append(vz)
sns.distplot(vz_maxwell,bins=20,hist=False,kde_kws={'linestyle':'--'})
x = np.linspace(0, 2000, 500)
plt.plot(x,(2*x*(MASS / 1000 / NA)/(2*kB*T_GAS))*np.exp(-(MASS / 1000 / NA)*x*x/(2*kB*T_GAS)))
plt.xlim((0, 2000))
plt.savefig("Ini_vz.png")
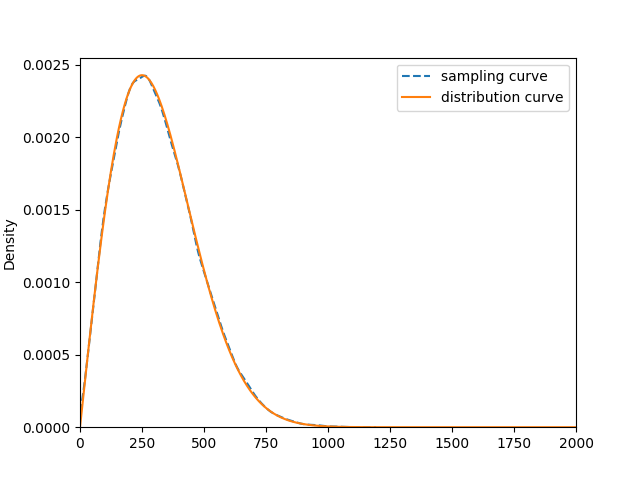
plt.show()结果如图:


测试评论邮件
升级ty1.2,每天发现新问题?
你好像没有邮件通知 我没收到?
热...热学的内容Σ(|||▽||| )大学物理里面会讲到的东西
你在说什么奇怪的话?