Julia的安装

Julia 语言扮演了这样一个角色：它是一门灵活的动态语言，适合用于科学计算和数值计算，并且性能可与传统的静态类型语言媲美。

Julia官网下载安装包

  1. https://julialang.org/downloads/
  2. 将安装路径加入path

在vscode中安装Julia插件

  1. https://code.visualstudio.com/download
  2. 如果插件没有自动找到Julia的位置而报错，到设置里Julia: Executable Path输入安装路径，要详细到\\bin\\julia.exe。（\用\\）

安装扩展包

安装General 注册表

  1. 安装了注册表才能安装General 注册表中记录的扩展包
  2. 打开julia.exe（或者在vscode中按F1,输入Julia: start REPL），按]，出现(@v1.4) pkg>
  3. 输入registry add https://mirrors.bfsu.edu.cn/git/julia-general.git（这是使用的BFSU北外镜像站安装，比从原始地址(Github)安装和更新要快一些）
  4. 安装完成image-20200720235009760
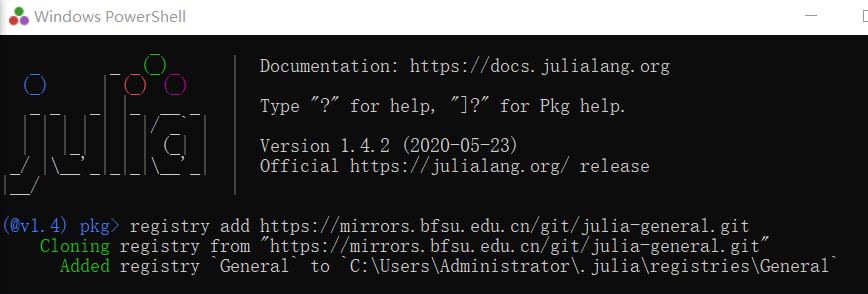
  5. General 的更新会走对应的镜像，而其他数据的下载则通过官方服务器(Pkg server：https://pkg.julialang.org)

安装DifferentialEquations扩展包

  1. DifferentialEquations.jl是个解微分方程的扩展包：https://diffeq.sciml.ai/dev/
  2. 输入add DifferentialEquations
  3. 安装image-20200721102807619
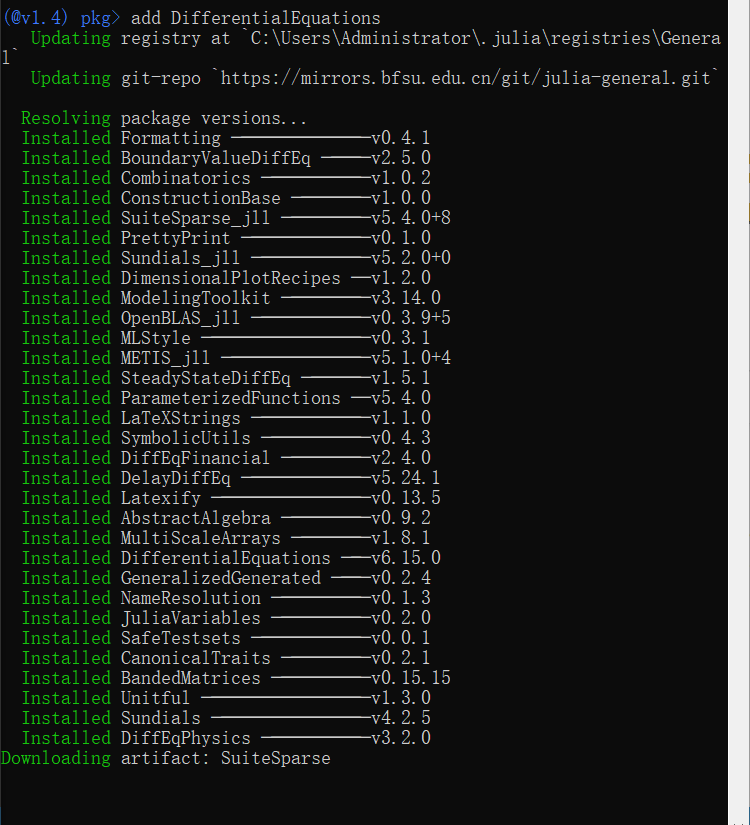
  4. 安装完成image-20200721102933940

安装DiffEqFlux扩展包

  1. DiffEqFlux.jl也是个解微分方程的扩展包：https://diffeqflux.sciml.ai/dev/
  2. 输入add DuffEqFlux
  3. 安装image-20200720235749070
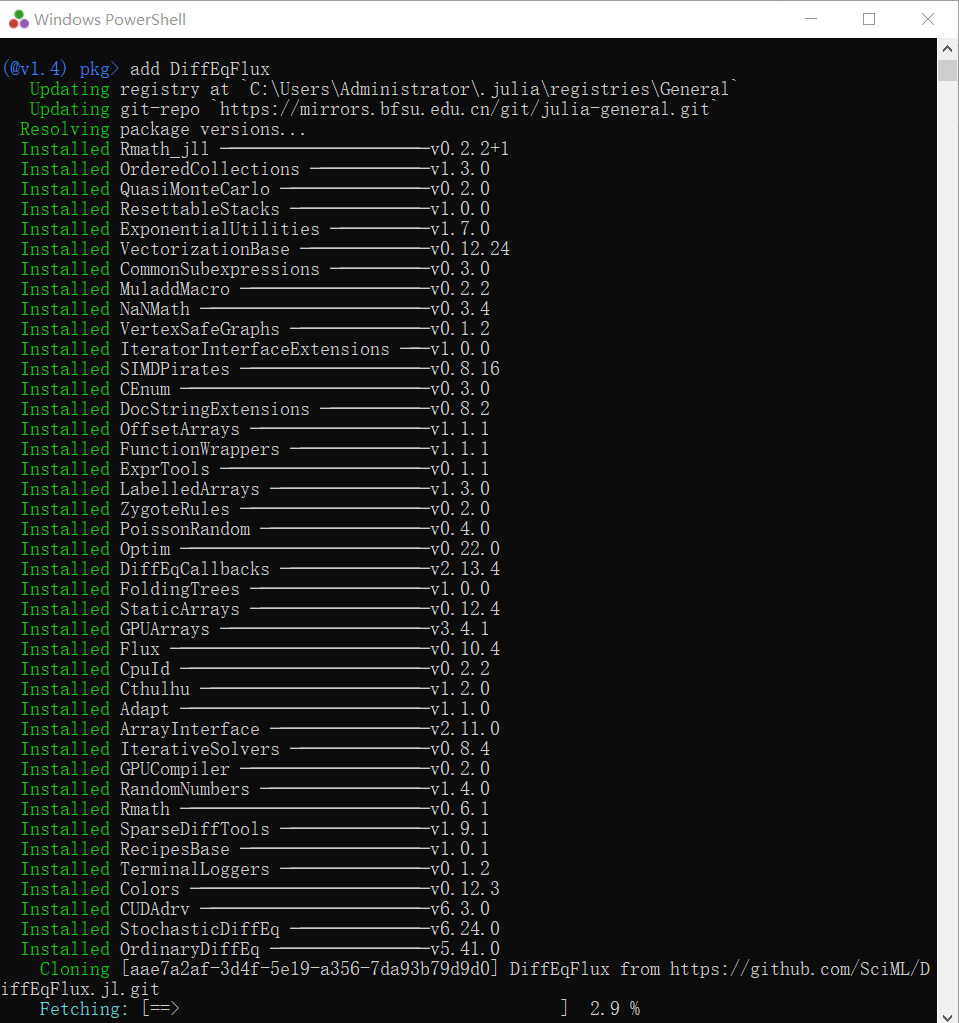
  4. 很长..很久之后…
  5. 安装完成image-20200721100926196

其他

如果跑代码的时候还报错说缺啥就补啥，总之扩展包都是在pkg模式下用add …，如果不小心断网又重装，可能导致没完全装好，用build …

Julia的使用

Julia解Lotka-Volterra方程组

$$ \frac{d x}{d t}=\alpha x-\beta x y $$

$$ \frac{d y}{d t}=-\delta y+\gamma x y $$

文件Lotka-Volterra.jl：

using DifferentialEquations, Flux, Optim, DiffEqFlux, DiffEqSensitivity

function lotka_volterra!(du, u, p, t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = α*x - β*x*y
  du[2] = dy = -δ*y + γ*x*y
end

# Initial condition
u0 = [1.0, 1.0]

# Simulation interval and intermediary points
tspan = (0.0, 10.0)
tsteps = 0.0:0.1:10.0

# LV equation parameter. p = [α, β, δ, γ]
p = [1.5, 1.0, 3.0, 1.0]

# Setup the ODE problem, then solve
prob_ode = ODEProblem(lotka_volterra!, u0, tspan, p)
sol_ode = solve(prob_ode, Tsit5())

# Plot the solution
using Plots
plot(sol_ode)
savefig("LV_ode.svg")

可以在vscode或者cmd中输入julia Lotka-Volterra，或者在julia REPL中输入julia> include("Lotka-Volterra.jl")。

LV_ode

Julia解 Lorenz方程组

$$ \frac{d x}{d t}=\sigma(y-x) $$

$$ \frac{d y}{d t}=x(\rho-z)-y $$

$$ \frac{d z}{d t}=x y-\beta z $$

文件Lorenz2.jl：

using DifferentialEquations, Plots
function parameterized_lorenz!(du,u,p,t)
    x,y,z = u
    σ,ρ,β = p
    du[1] = dx = σ*(y-x)
    du[2] = dy = x*(ρ-z) - y
    du[3] = dz = x*y - β*z
end

u0 = [1.0,0.0,0.0]
tspan = (0.0,100.0)
p = [10.0,28.0,8/3]
prob = ODEProblem(parameterized_lorenz!,u0,tspan,p)
sol = solve(prob)

plot(sol,vars=(1,2,3))
savefig("L2_ode.svg")

可以在vscode或者cmd中输入julia Lorenz2，或者在julia REPL中输入julia> include("Lorenz2.jl")。

运行环境为笔记本电脑，win10专业版，64位，CPU: Intel(R) Core(TM) i7-6700HQ CPU @ 2.60GHz，8核，RAM 8G，Julia Version 1.4.2，运行时长大约110s左右。

[Running] julia "e:\Julia\Lorenz2.jl"

[Done] exited with code=0 in 114.155 seconds

L2_ode

Julia解二阶常微分方程

$$ \ddot{\theta}+\frac{g}{L} \sin (\theta)=0 $$

# Simple Pendulum Problem
using OrdinaryDiffEq, Plots

#Constants
const g = 9.81
L = 1.0

#Initial Conditions
u₀ = [0,π/2]
tspan = (0.0,6.3)

#Define the problem
function simplependulum(du,u,p,t)
    θ = u[1]
    dθ = u[2]
    du[1] = dθ
    du[2] = -(g/L)*sin(θ)
end

#Pass to solvers
prob = ODEProblem(simplependulum, u₀, tspan)
sol = solve(prob,Tsit5())

#Plot
plot(sol,linewidth=2,title ="Simple Pendulum Problem", xaxis = "Time", yaxis = "Height", label = ["\\theta" "d\\theta"])
savefig("2nd-Order.svg")

p = plot(sol,vars = (1,2), xlims = (-9,9), title = "Phase Space Plot", xaxis = "Velocity", yaxis = "Position", leg=false)
function phase_plot(prob, u0, p, tspan=2pi)
    _prob = ODEProblem(prob.f,u0,(0.0,tspan))
    sol = solve(_prob,Vern9()) # Use Vern9 solver for higher accuracy
    plot!(p,sol,vars = (1,2), xlims = nothing, ylims = nothing)
end
for i in -4pi:pi/2:4π
    for j in -4pi:pi/2:4π
        phase_plot(prob, [j,i], p)
    end
end
plot(p,xlims = (-9,9))
savefig("2nd-Order2.svg")
[Running] julia "e:\Julia\2nd-Order.jl"

[Done] exited with code=0 in 84.122 seconds

2nd-Order

2nd-Order2

Julia解Hénon_Heiles方程组

$$ \frac{d^{2} x}{d t^{2}}=-\frac{\partial V}{\partial x} $$

$$ \frac{d^{2} y}{d t^{2}}=-\frac{\partial V}{\partial y} $$

其中

$$ V(x, y)=\frac{1}{2}\left(x^{2}+y^{2}+2 x^{2} y-\frac{2}{3} y^{3}\right) $$

using OrdinaryDiffEq, Plots

#Setup
initial = [0.,0.1,0.5,0]
tspan = (0,100.)

#Remember, V is the potential of the system and T is the Total Kinetic Energy, thus E will
#the total energy of the system.
V(x,y) = 1//2 * (x^2 + y^2 + 2x^2*y - 2//3 * y^3)

#Define the function
function Hénon_Heiles(du,u,p,t)
    x  = u[1]
    y  = u[2]
    dx = u[3]
    dy = u[4]
    du[1] = dx
    du[2] = dy
    du[3] = -x - 2x*y
    du[4] = y^2 - y -x^2
end

#Pass to solvers
prob = ODEProblem(Hénon_Heiles, initial, tspan)
sol = solve(prob, Vern9(), abs_tol=1e-16, rel_tol=1e-16);

# Plot the orbit
plot(sol, vars=(1,2), title = "The orbit of the Hénon-Heiles system", xaxis = "x", yaxis = "y", leg=false)
savefig("HH_ode.svg")
[Running] julia "e:\Julia\Hénon-Heiles.jl"

[Done] exited with code=0 in 68.487 seconds

HH_ode

以上例子出自：