晶体表示方法

AI摘要：The article discusses the representation of crystals, their basic concepts, and classification. It explains the difference between crystals and non-crystals, the ideal shapes of crystals, and the Miller index for crystal planes. The article also covers the basic symmetry of crystals, the seven crystal systems, the 14 Bravais lattices, and the 32 crystal point groups.

Powered by AISummary and Kimi.

由结构基元（原子、离子、分子等）进行三维长程有序排列而构成的一切固体物质都是晶体。晶体与非晶体之间的主要差别在于它们是否有三维长程点阵结构。

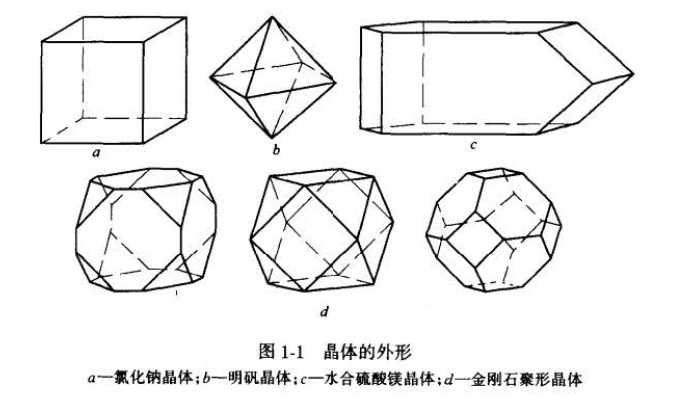
晶体可以有单形和聚形两种理想外形。单形是由形状、大小、面指数相同的晶面构成的晶体外形，如六面体（氯化钠）、正八面体（明矶）等（见图1 - 1 a和b) 。晶体共有47种单形。聚形是由两种或两种以上的晶面构成的晶体外形，如方柱多面体（水合硫酸镁，见图1 - 1 c) 。

平行六面体是空间三维物体周期性重复的基本单元，或称单胞；决定该单胞的基本参数是平行六面体的三个边长a 、b、c和三边间的夹角α、β、γ。

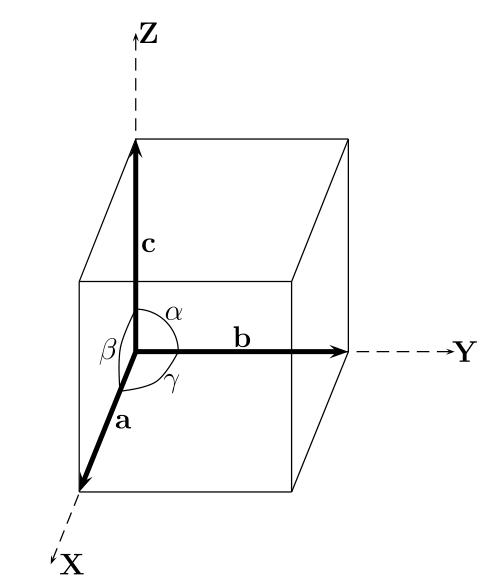
米勒指数(Miller index)

晶体中的晶面表示含有多于三个质点的平面。假如一个晶面与X，Y，Z轴相交的长度r, s, t; 分别取其倒数1/r, 1/s, 1/t，并对这三个分数进行通分；通分后三个分数的分子就是这个晶面的晶面指数h k l，也称米勒指数。（当晶面和晶轴平行时，该数值为0；当晶面与某一晶轴的负方向相交，则相应的指数上加一个 $ \bar{} $ ）

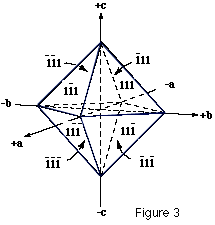
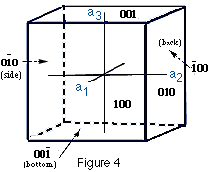
若考虑到晶体所具有的对称性，有许多不平行的晶面上也具有相同的质点分布。这些晶面是彼此等同的，我们把它们称作一个晶面族，记做{h k l}。例如在立方晶系中，{1 0 0}包含 $ (100) $ 、 $ (010) $ 、 $ (001) $ 、 $ (\bar100) $ 、 $ (0\bar10) $ 、 $ (00\bar1) $ 共六种晶面。

晶向是指在晶体中任何一条穿过许多质点的直线方向。晶体中不同的晶向，常常具有不同的线密度等不同属性。为区分晶体这些晶向，结晶学上人们引入晶向指数，用[m n w]表示晶向上某质点原子坐标的最简整数比。

考虑晶体对称性，也有若干个晶向常常是等同的。它们构成一个晶向族，用\<m n w\>来表示这一系列的晶向。例如：对于立方晶系，<100>包含六个晶向： $ [100] $ 、 $ [010] $ 、 $ [\bar100] $ 、$ [0\bar10] $ 、 $ [001] $ 、 $ [00\bar1] $ ；在立方晶系中，由于晶胞参数(a, b, c)的特殊关系，某一晶面(h k l)与指数相同的晶向[h k l]恰好垂直。

中括号[]表示的是晶体中的晶向
尖括号<>表示的是晶向族
圆括号（）表示的是晶面的密勒指数（晶面指数；Miller指数）
花括号｛｝表示的是晶面族

晶体的基本对称性

人们定义使各原子的位置发生变换，变换后晶体的结构状态与变换前正好相同的操作称为对称操作。晶体基本的对称操作有点操作和平移操作。

在一般的对称操作过程中，空间有许多点在动，且操作前后状态一样。但点操作要求操作中至少有一个点不动。在对称操作过程中保持空间至少有一个不动点的操作称为点对称操作。具体的点对称操作有恒等操作、平面反映操作、旋转操作、反演操作和旋转反演操作，其中平面反映和旋转反演操作属于复合操作。旋转轴只能是1次、2次、3次、4次和6次的；平面反映操作也称为镜面操作 $ m $ ，它等同于一个2次旋转反演操作 $ \bar2 $ 。反演操作为 $ \bar1 $ ，其他的旋转反演操作可为 $ \bar3 $ 、 $ \bar4 $ 、 $ \bar6 $ 。相对应的对称操作元素分别为镜面、旋转轴、反演中心、旋转反演轴等，恒等操作没有对称操作元素。在三维空间内若能通过旋转把一个位置转换到另一位置，则这两个位置彼此同宇。

在三维空间内若能通过旋转把一个位置转换到另一位置，则这两个位置彼此同宇。否则这两个位置是不同宇的，不同宇的两个位置间一定经历了奇数个反演操作。这里可以借助左、右手的关系理解同宇的概念。旋转操作作用于左手时，不论怎样的旋转都不能把左手转成右手；而带有一次反演的操作则可以把左手转变成右手，如平面反映就可以把左手转变成右手。左手和右手呈镜面对称，是不同宇的。

已知在晶体学中只允许有5种旋转对称操作，其转角为 $ \frac{2\pi}{n} $ ，且有n=1,2,3,4,6；相应的熊夫利斯符号为 $ C_1(E) $ 、 $ C_2 $ 、 $ C_3 $ 、 $ C_4 $ 和 $ C_6 $ 。其他的晶体旋转不能适当地填满空间。由于n值的限制，可能的旋转反演对称操作也只能有了 $ \bar1 $ （反演）、 $ \bar2 $ （m,平面反映）、 $ \bar3 $ 、 $ \bar4 $ 和 $ \bar6 $ ；相应的熊夫利斯符号为 $ i $ 、 $ \sigma $ 、 $ S_6 $ 、 $ S_4 $ 和 $ C_{3h} $ 。

分子对称性可分成5种对称元素。
旋转轴：分子绕轴旋转 $ \frac{360^\circ}{n} $ 度角后与原分子重合，此轴也称为n重旋转轴，简写为$C_n$。例如水分子是 $ C_2 $ 而氨是 $ C_3 $ 。一个分子可以拥有多个旋转轴；有最大n值的称为主轴，为直角坐标系的z轴，较小的则称为副轴。n≥3的轴称高次轴。
对称面：一个平面反映分子后和原分子一样时，此平面称为对称面。对称面也称为镜面，记为$σ$。水分子有两个对称面：一个是分子本身的平面，另一个是垂直于分子中心的平面。包含主轴，与分子平面垂直的对称面称为垂直镜面，记为 $ σ_v $ ；而垂直于主轴的对称面则称为水平镜面，记为 $ σ_h $ 。等分两个相邻副轴夹角的镜面称等分镜面，记作 $ σ_d $ 。一个对称面可以笛卡尔坐标系识别，例如(xz)或(yz)。
对称中心：从分子中任一原子到分子中心连直线，若延长至中心另一侧相等距离处有一个相同原子，且对所有原子都成立，则该中心称为对称中心，用 $ i $ 表示。对称中心可以有原子，也可以是假想的空间位置。例如四氟化氙（ $ XeF_4 $ ）的对称中心位于Xe原子，而苯（ $ C_6H_6 $ ）的对称中心则位于环的中心。
旋转反映轴：分子绕轴旋转 $ \frac{360^{\circ}}{n} $ 度，再相对垂直于轴的平面进行反映后分子进入等价图形，记为 $ S_n $ 。该操作是旋转与反映的复合操作，例子有四面体型的含有三个 $ S_4 $ 轴的四氟化硅，以及有一个 $ S_6 $ 轴的乙烷的交叉式构象。
恒等元素：简写为E，取自德语的Einheit，意思为“一”。恒等操作即分子旋转360°不变化的操作，存在于每个分子中。这个元素似乎不重要，但此条件对群论机制和分子分类却是必要的。

7种晶系

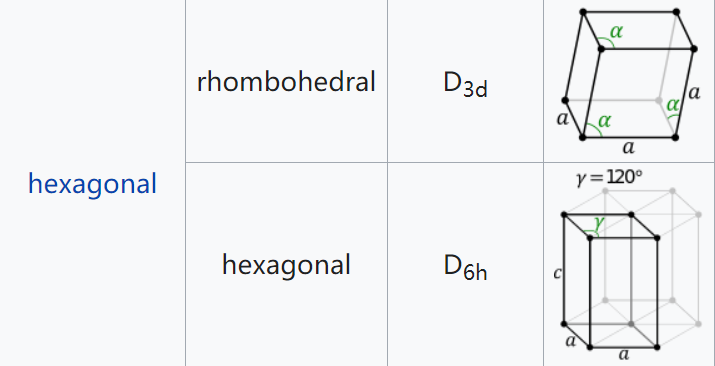
根据实际晶体主要的点对称特征可以把所有晶体划分成7种晶系。

表中表示对称性的符号是国际符号，括号内符号则是相应的熊夫利斯符号。特别要注意的是，边、角关系中不等号＂≠＂的意思是指对称条件不要求这里是等号，并不是说不允许相等。

晶体所具有的点对称性决定了晶体所属的晶系，而不是其单胞的边角关系。

14种布拉菲点阵

在空间中由几何点即阵点排列成的无限阵列，其中每一点与其他所有的这种点有完全相同的环境，这种阵列称为点阵(Lattice)。所有晶体都具有平移不变性，或称平移对称性。借助点的平移可产生这种点阵。晶体被定义为原子的三维长程有序排列，即周期性排列。所谓周期性就是平移对称性。平移对称性可理解为点平移后其环境不变。三维空间内单位平移矢量构成的平行六面体即为点阵的单胞。若单胞只含有一个阵点则称为初基单胞。

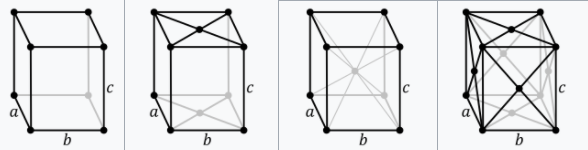
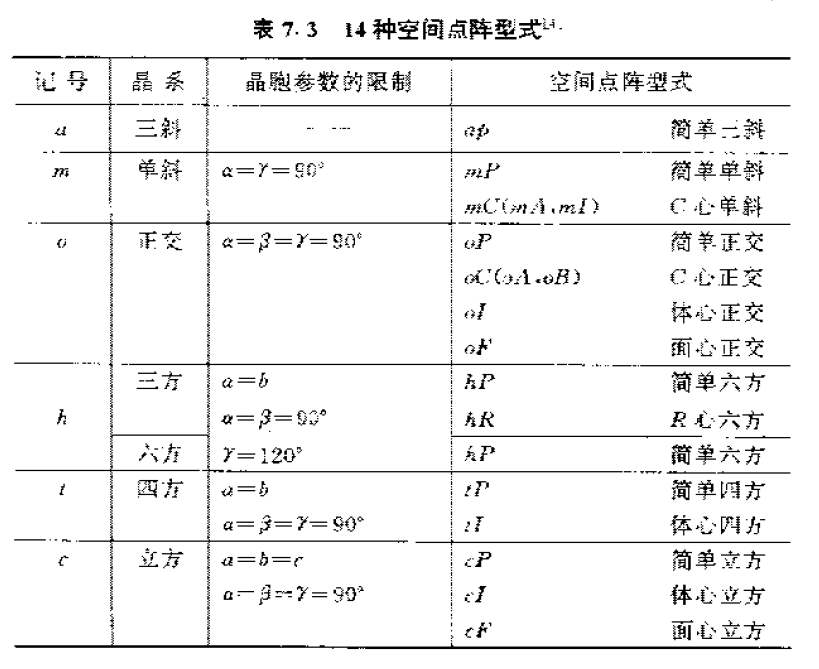
7 种晶系是从点对称性的角度出发对所有晶体做粗略划分。若从晶体的平移对称特性出发，则所有晶体可能具有14 种不同的点阵，或称为14 种以法国晶体学家A.Bravais命名的布拉菲点阵。

设有某一点阵，若用其初基单胞即可反映出该点阵的平移对称性，又可反映出相应晶系所具有的点对称特征对初基单胞边角关系的限制，则这种点阵称为初基点阵。初基点阵所展示的平移矢董为初基平移矢量。参照前文表1-1所示各晶系单胞边角关系，可以得出7种初基布拉菲点阵，每种晶系对应一个初基点阵。应注意的是，三方晶系取六角坐标系时与六方晶系的平移对称性相同，因此它们对应的点阵是等价的；这些初基点阵用P作为标记。P也代表它们的初基单胞或称P单胞。对三方晶系还存在一种菱形单胞的初基点阵，用R作为标记(R表示菱面体， Rhombohedron)。另外，还有其他7种布拉菲点阵。这7种点阵是在原初基点阵内加人一些新的阵点，通过点阵有心化而获得。阵点不能随意加人，加人新阵点后，首先要看新的阵点排列是否还构成点阵，即这一点阵是否可以形成无限阵列并且所有阵点都有完全相同的环境；同时所得到的点阵还应确实是一个新的点阵。这类新点阵的单胞变成了多个阵点的复式单胞，属于非初基单胞。这种单胞形式也能够体现出相应晶系所具有的点对称特征对其单胞边角关系的限制。

在讨论上述7种初基点阵以外的其他布拉菲点阵时，使用这种复式单胞很方便，所以常被人们采纳，被称为惯用单胞。在这种点阵划分方法中，一方面，凡属于同一晶系的空间点阵都选用相同的参考轴，所以全部惯用的复式单胞都可以表现出与相应的初基点阵单胞相同的点对称特征和相应的平移对称性；另一方面，由复式单胞构成的新点阵中仍可找出只有一个阵点的初基单胞，并且可以通过该初基单胞的点阵矢董平移将整个空间点阵再现出来。但是这种单胞本身不能以简洁清晰的方式反映出晶系主要的点对称特征对其单胞边角关系的限制。点对称性对于晶体结构分析十分重要，需要从单胞上直接反映出来，以使入们很容易想像出晶体的结构特征，所以研究晶体结构时对有心点阵通常不选用其初基单胞，而选用复式单胞。但有心点阵的初基平移矢量仍取其初基单胞的平移矢量。下表给出了描述晶体平移对称性的14种布拉菲点阵，其中初基P和R点阵的单胞只有一个阵点，体心I点阵的单胞有两个阵点，面心F点阵的单胞有四个阵点，底心C或B点阵的单胞有两个阵点。

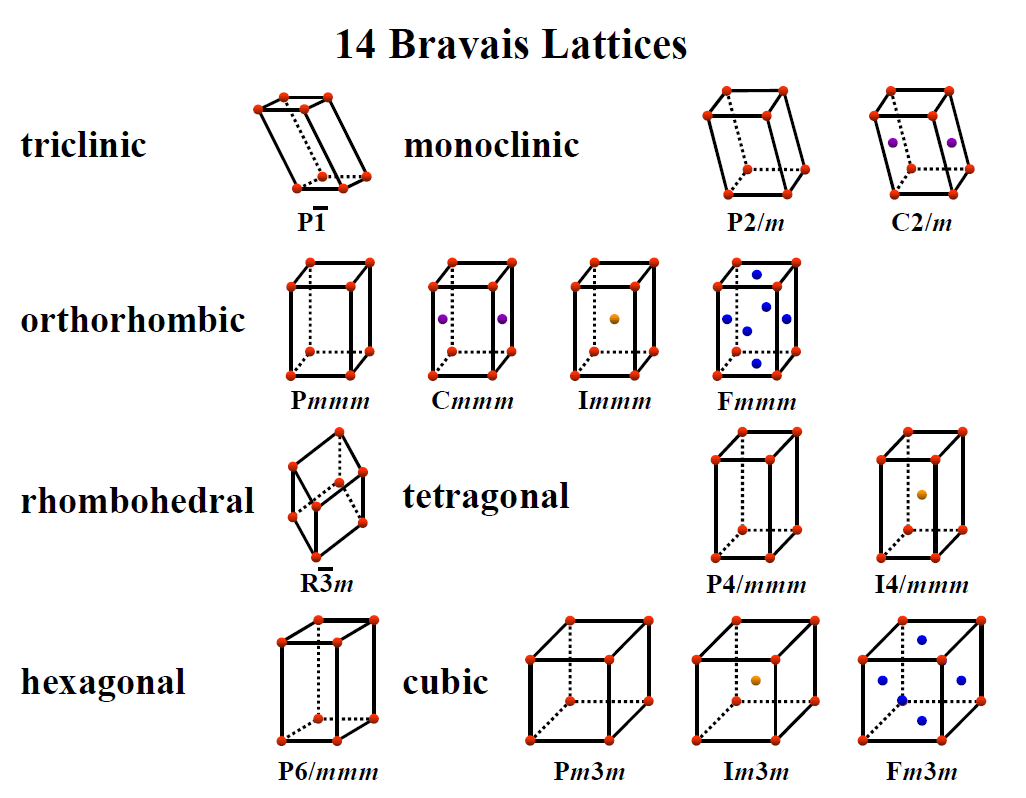
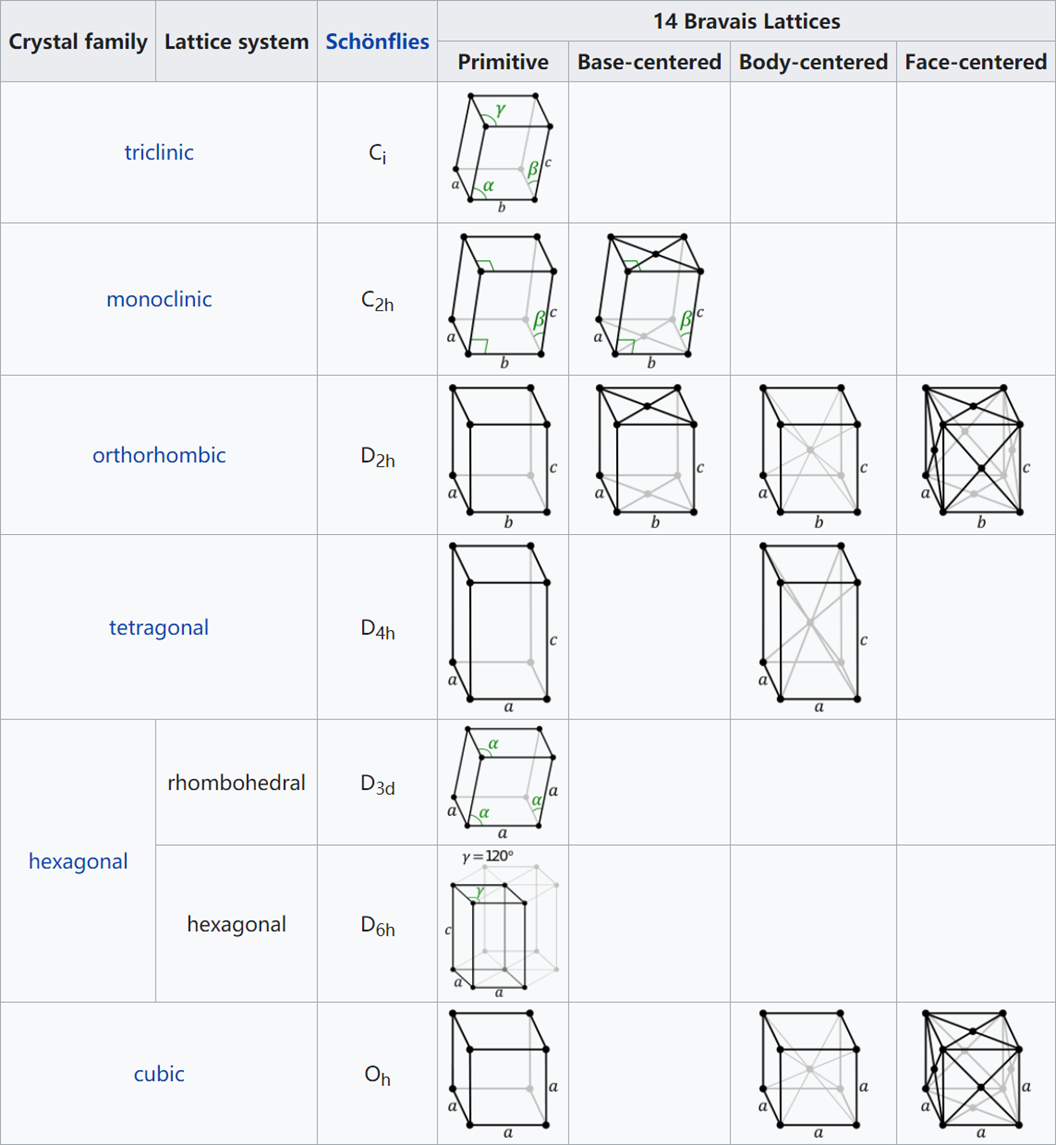
点阵所表达的晶体平移对称性包括晶体内每一个原子的平移对称性，也包括各原子间每一个空隙位置的平移对称性。因此，点阵是实际晶体所具备的平移对称性的高度抽象和概括，点阵内阵点与阵点之间的关系等同于实际晶体内所具有相应平移对称性几何点之间的关系。切忌把阵点只是简单地理解成真实晶体中原子的位置。实际上，有很多种晶体单胞在其所对应的点阵单胞的阵点位置上并没有原子。

a--anorthic, m--monoclinic, o--orthorhombic, h--hexagonal(rhombohedral & hexagonal), t--tetragonal ,c--cubic.
简单P(Primitive)，底心S或C或B或A(Base-centered)，体心I(Body-centered)，面心F(Face-centered)
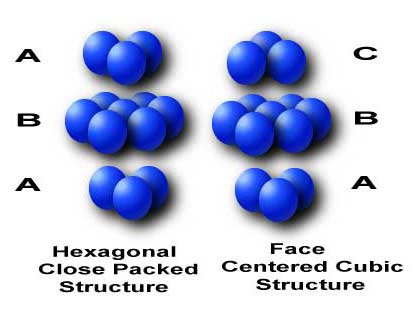
fcc：face-centered cubic structure 面心立方结构
hcp：hexagonal close-packed structure 密排六方结构
bcc：body-centered cubic structure 体心立方结构

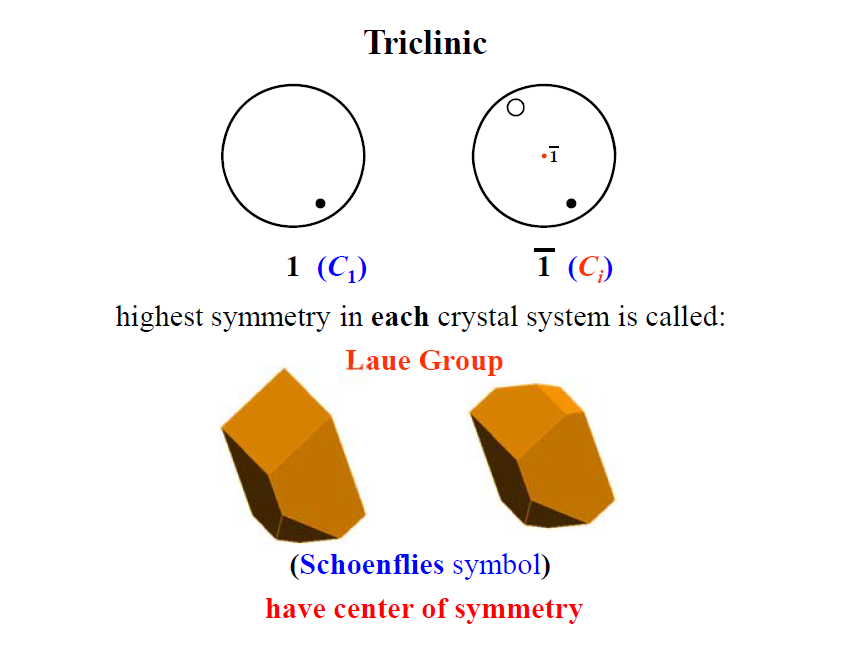
晶体学点群

经典晶体学认为，点对称操作的组合可以描述所有规则几何外形单晶体所具备的点对称性。但许多金属单晶体虽然不一定具备规则的几何外形，但它们相应的点对称性却仍然存在。因此近代晶体学出现之后，人们认识到晶体的点对称性实质上反映了晶体内部结构的点对称性，只有在特定的单晶生长条件下晶体的点对称性才反映在几何外形上。

点对称操作的集合符合群的条件。群内对称操作的个数为群的阶，用h表示。对称操作组合在一起操作时，空间几乎所有点都在变动，但至少有一个点（如原点）在全部对称操作过程中始终保持不变。它也是所有对称元素的一个公共点。所以把点对称操作的集合所构成的群称为点群。通常，阶数越高的点群其对称性越高。点群以高度的数学抽象方式表述了实际晶体的点对称性。

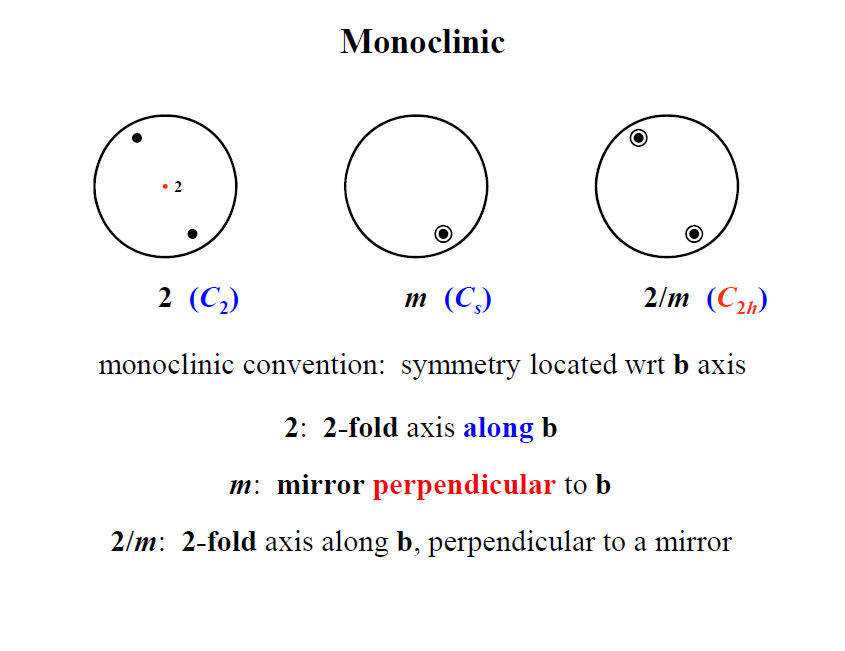
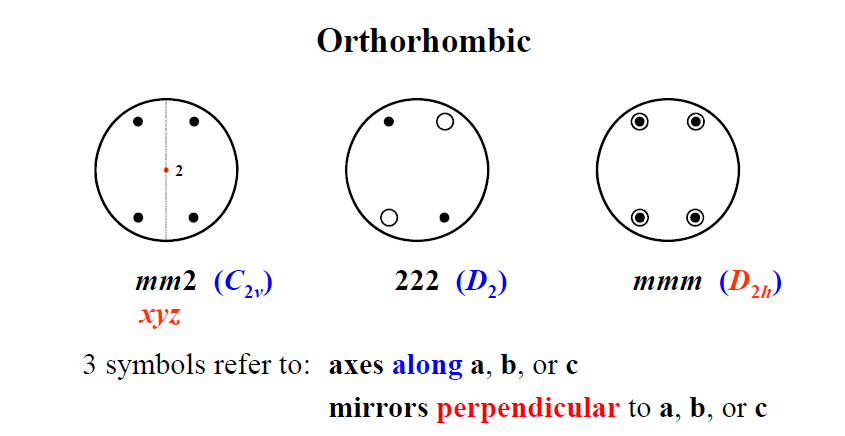
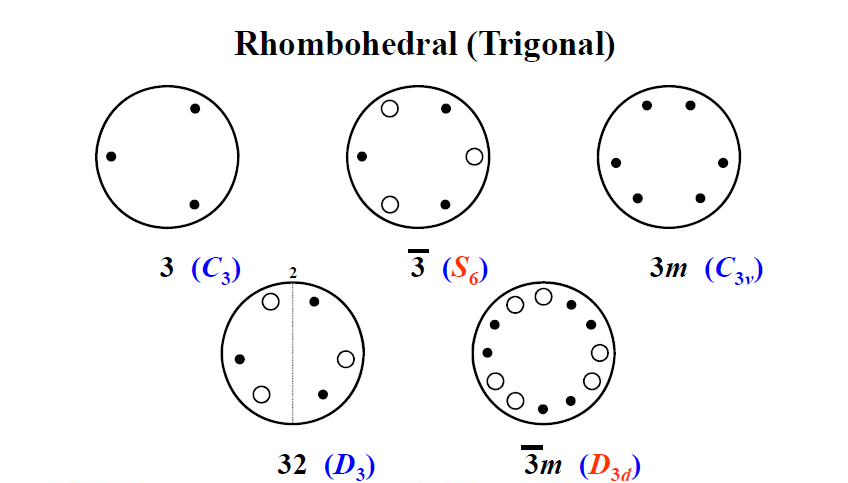
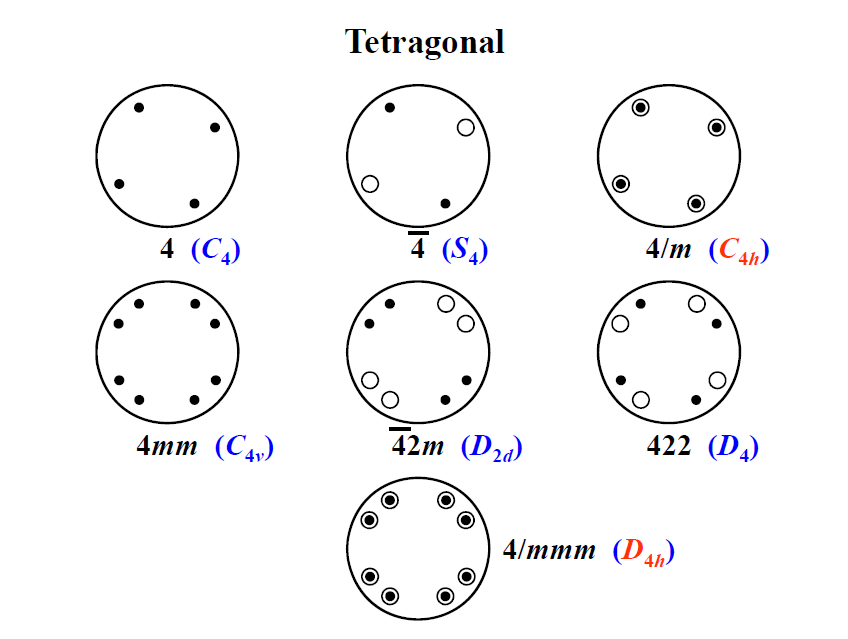
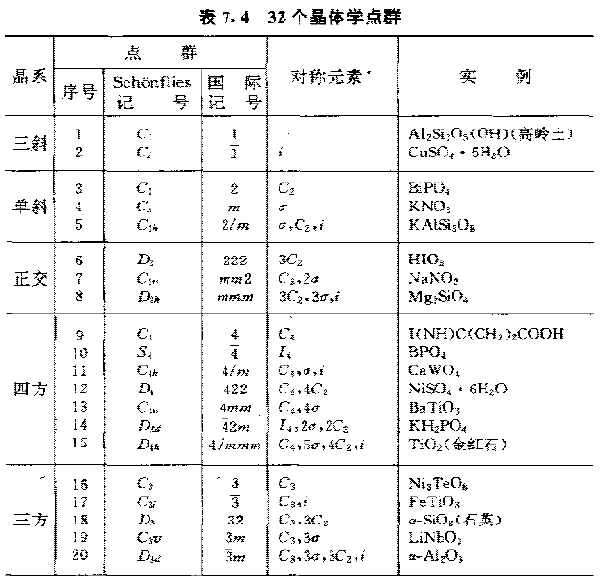
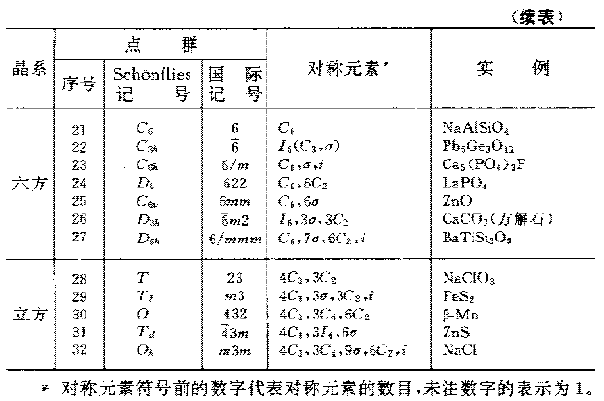
1830 年以后，人们才发现晶体共有32 种晶类，每一种晶类对应着一种点群。

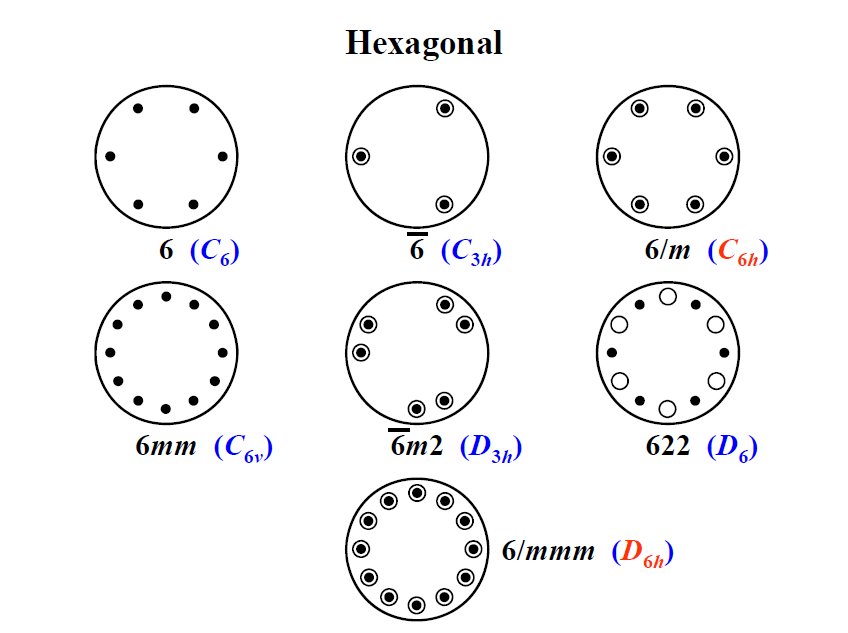
可以用不同的方法推导32种点群：(1)从7种晶系的主要点对称特征出发外延推演，可以推导出32种点群。这种推导方法的优点在于点群与晶系的对应关系十分明确。(2)旋转群推导法，即先推导11种纯旋转晶体学点群，然后与反演操作组合可得11种中心对称的晶体学点群，再推导出另外10种非中心对称的点群，共得32种点群。这种方法的优点在于可以很快完成推导。(3)循环群推导法，是先确定5 种循环群 $ 1(C_1) $ , $ 2(C_2) $ , $ 3(C_3) $ , $ 4(C_4) $ 和 $ 6(C_6) $ ，再在每种循环群上加进各种新对称操作，或用 $ \bar{n} $ 取代 $ n $ 轴，这样也可以推导出32种点群。其优点在于通过推导可以更为透彻地了解各种点群的对称操作。

熊夫利斯符号表示点群：
$ C_n $ （循环群）表示该群有一根n次旋转轴。 $ C_{nh} $ 是 $ C_n $ 加上一个与旋转轴垂直的镜面（反映）对称元素。 $ C_{nv} $ 则是 $ C_n $ 加上一个与旋转轴平行的镜面对称元素。
$ S_{2n} $ （源自德语Spiegel，意思是镜面）表示一根只含有2n次旋转反映轴（简称映轴）。
$ D_n $ （二面体群）表示这个群只有一根n次旋转轴和n根垂直于这根主轴的二重轴。 $ D_{nh} $ 是加上一个与n次旋转轴垂直的镜面。 $ D_{nd} $ 则是 $ D_n $ 是加上n个与n次旋转轴平行的镜面。
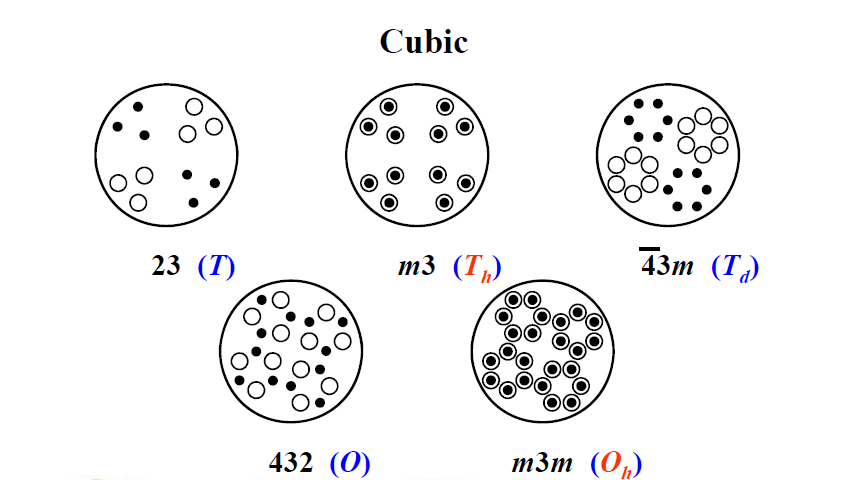
字母 $ T $ （四面体）表示这个群有四面体的对称性。 $ T_d $ 则包括了旋转反映操作， $ T $ 群本身则不包含旋转反映操作， $ T_h $ 则是 $ T $ 群加上与旋转轴垂直的镜面。
字母 $ O $ （八面体）表示该群具有八面体或者立方体的对称性，可能包括（ $ O_h $ ）或不包括（ $ O $ ）旋转反映操作。